命题逻辑

命题逻辑主要研究前提和结论之间的逻辑关系

命题

定义

一个具有真或假但不能两者都是的断言（陈述句）称为命题
常用大写字母 $A,B,C,\cdots$ 表示命题，如命题 $P$：明天下雨
如果一个命题所表达的判断为真，则称其真值为“真”，用大写字母 T 或数字 1 表示
如果一个命题所表达的判断为假，则称其真值为“假”，用大写字母 F 或数字 0 表示

由定义可知，命题需要满足以下条件：

• 表达判断的陈述句
• 具有确定的真假值

分类

依据命题的繁简

简单命题

不包含其他更简单的命题称为简单命题，又称原子命题

如：命题“钓鱼岛是中国的”就是一个简单命题，它不含有更简单的命题了

复合命题

由简单命题和联结词组合而成的命题称为复合命题

如：命题“如果明天不下雨，那么我去郊游”为一个复合命题，因为它是命题“明天不下雨”和命题“我去郊游”的组合

命题常元与命题变元

一个表示确定命题的符号称为命题常元，通常根据其真值用 $T$ 或 $F$ 表示；一个可泛指任意命题的符号称为命题变元，也称命题变量、句子变量，通常用大写字母 $A,B,C,\cdots$ 表示
命题常元可类比为实数域中的常数，如 $\pi$；命题变元可类比为实数域中的变量，如 $x$
命题变元的取值要么是 $T$ 要么是 $F$，即命题常元的集合；就像变量 $x$ 的取值是实数域中的数一样，是所有实常数的集合

显然，命题变元不是命题，因为它的真值不定（只有用一个特定命题才能得知）

联结词

在代数中，用 $+,-,\times,\div$ 等运算符连接数字得到代数表达式，如 $57+1226$
而在数理逻辑中，也存在运算符，称为逻辑联结词，简称联结词
因此联结词实质上是数理逻辑的运算符

在汉语中，常用的联结词有“非”、“与”、“或”、“如果······那么······”、“当且仅当”等
而数理逻辑中也有与之对应的联结词

数理联结词	汉语中与之对应的词	表示符号	示例
否定联结词	非	$\lnot$	$\lnot P$
合取联结词	与 和 且	$\land$	$P\land Q$
析取联结词	或	$\lor$	$P\lor Q$
条件联结词	如果······，那么······ 只要······，就·····	$\rightarrow$	$P\rightarrow Q$
双条件联结词	当且仅当	$\leftrightarrow$	$P\leftrightarrow Q$

优先次序：$\lnot$ 优先级最高，$\land,\lor$ 次之，$\rightarrow,\leftrightarrow$ 优先级最低；相同优先级的联结词按从左到右顺序

联结词种类

否定联结词

$P$ 为命题，则“非 $P$” 是复合命题，记作 $\lnot P$
其中：$\lnot$ 表示否定联结词的符号

$\lnot P$ 为真，当且仅当 $P$ 为假

下面是否定联结词的真值表：

$P$	$\lnot P$
0	1
1	0

合取联结词

$P,Q$ 是命题，则 “$P$ 且 $Q$” 是复合命题，记作 $P\land Q$
其中：$\land$ 表示合取联结词的符号

$P\land Q$ 为真，当且仅当 $P,Q$ 都为真

下面是合取联结词的真值表：

$P$	$Q$	$P\land Q$
0	0	0
0	1	0
1	0	0
1	1	1

析取联结词

$P,Q$ 是命题，则 “$P$ 或 $Q$” 是复合命题，记作 $P\lor Q$
其中：$\lor$ 表示析取联结词的符号

$P\lor Q$ 为真，当且仅当 $P,Q$ 至少有一个为真

下面是析取联结词的真值表：

$P$	$Q$	$P\lor Q$
0	0	0
0	1	1
1	0	1
1	1	1

条件联结词

$P,Q$ 是命题，则“如果 $P$ 那么 $Q$” 是复合命题，记作 $P\rightarrow Q$
其中：$\rightarrow$ 表示条件联结词的符号
称：

• $P$ 为假设或前件
• $Q$ 为结论或后件

$P\rightarrow Q$ 为假，当且仅当 $P$ 为真 $Q$ 为假

下面是条件联结词的真值表：

$P$	$Q$	$P\rightarrow Q$
0	0	1
0	1	1
1	0	0
1	1	1

$P\rightarrow Q\Leftrightarrow\lnot P\lor Q$
其中 $\Leftrightarrow$ 为等价符号，详见等价

为什么这么定义？下面举例详细说明：
如果我说：“如果明天不下雨，那么我去爬山”
不妨设 $P$：明天不下雨，$Q$：我去爬山，$P\rightarrow Q$：如果明天不下雨，那么我去爬山
如果实际情况是：明天不下雨（$P$ 为 $1$），而且我去爬山了（$Q$ 为 $1$），可知我说的这句话是真的（$P\rightarrow Q$ 为 $1$）
如果实际情况是：明天不下雨（$P$ 为 $1$），但是我没去爬山（$Q$ 为 $0$），可知我说的这句话是假的（$P\rightarrow Q$ 为 $0$）
以上这两种情况都很好理解
如果实际情况是：明天下雨（$P$ 为 $0$），那么不管我有没有去爬山你都不能说我说的这句话是假的，也不能说是真的。因为假设都没满足
但是如果我们反过来，假设我说的话是真的（$P\rightarrow Q$ 为 $1$），如果假设为假（$P$ 为 $0$），那么结论的真假未知（可真可假）

双条件联结词

$P,Q$ 是命题，则“$P$ 当且仅当 $Q$” 是复合命题，记作 $P\leftrightarrow Q$
其中：$\leftrightarrow$ 表示双条件联结词的符号

$P\leftrightarrow Q$ 为真，当且仅当 $P,Q$ 的真值相同

下面是双条件联结词的真值表：

$P$	$Q$	$P\leftrightarrow Q$
0	0	1
0	1	0
1	0	0
1	1	1

$P\leftrightarrow Q\Leftrightarrow(P\rightarrow Q)\land(Q\rightarrow P)$

条件否定联结词

$\nrightarrow$ 表示条件否定联结词的符号

$P\nrightarrow Q$ 为真，当且仅当 $P$ 为真 $Q$ 为假

下面是条件否定联结词的真值表：

$P$	$Q$	$P\nrightarrow Q$
0	0	0
0	1	0
1	0	1
1	1	0

$P\nrightarrow Q\Leftrightarrow \lnot(P\rightarrow Q)$

异或联结词

$\oplus$ 表示异或联结词的符号

$P\oplus Q$ 为真，当且仅当 $P,Q$ 真值不同

下面是异或联结词的真值表：

$P$	$Q$	$P\oplus Q$
0	0	0
0	1	1
1	0	1
1	1	0

$P\oplus Q\Leftrightarrow\lnot(P\leftrightarrow Q)$

或非联结词

$\downarrow$ 表示或非联结词的符号

$P\downarrow Q$ 为真，当且仅当 $P,Q$ 都为假

下面是或非联结词的真值表：

$P$	$Q$	$P\downarrow Q$
0	0	1
0	1	0
1	0	0
1	1	0

$P\downarrow Q\Leftrightarrow\lnot(P\lor Q)$

与非联结词

$\uparrow$ 表示与非联结词的符号

$P\uparrow Q$ 为假，当且仅当 $P,Q$ 都为真

下面是与非联结词的真值表：

$P$	$Q$	$P\uparrow Q$
0	0	1
0	1	1
1	0	1
1	1	0

$P\uparrow Q\Leftrightarrow\lnot(P\land Q)$

联结词的完备集

下面证明以上 9 个联结词能表达所有命题
命题可以符号化为命题公式，而由命题公式的递归定义的条款 2 可知命题公式只包含一元和二元运算符

1. 对于一元运算符
   一元运算符只作用于一个命题变元 $P$，有四种可能的结果

   $P$	$\begin{matrix}f_1&f_2&f_3&f_4\end{matrix}$
   $0$	$\begin{matrix}0&~~0&~1&~~1\end{matrix}$
   $1$	$\begin{matrix}0&~~1&~0&~~1\end{matrix}$

   其中，$f_1P\Leftrightarrow F$，$f_2P\Leftrightarrow P$，$f_3P\Leftrightarrow\lnot P$，$f_3P\Leftrightarrow T$
   可见，对于一元运算符的每一种运算结果都能用以上 9 个联结词表达

2. 对于二元运算符
   二元运算符只作用于两个命题变元 $P,\ Q$，有十六种可能的结果

   $P$	$Q$	$\begin{matrix}f_1&f_2&f_3&f_4&f_5&f_6&f_7&f_8&f_9&f_{10}&f_{11}&f_{12}&f_{13}&f_{14}&f_{15}&f_{16}\end{matrix}$
   $0$	$0$	$\begin{matrix}0&~~0&~0&~~0&~0&~~0&~0&~~0&~1&~~~1&~~~1&~~~1&~~~1&~~~1&~~~1&~~~1\end{matrix}$
   $0$	$1$	$\begin{matrix}0&~~0&~0&~~0&~1&~~1&~1&~~1&~0&~~~0&~~~0&~~~0&~~~1&~~~1&~~~1&~~~1\end{matrix}$
   $1$	$0$	$\begin{matrix}0&~~0&~1&~~1&~0&~~0&~1&~~1&~0&~~~0&~~~1&~~~1&~~~0&~~~0&~~~1&~~~1\end{matrix}$
   $1$	$1$	$\begin{matrix}0&~~1&~0&~~1&~0&~~1&~0&~~1&~0&~~~1&~~~0&~~~1&~~~0&~~~1&~~~0&~~~1\end{matrix}$

   其中，$Pf_1Q\Leftrightarrow F$，$Pf_2Q\Leftrightarrow P\land Q$，$Pf_3Q\Leftrightarrow P\nrightarrow Q$，$Pf_4Q\Leftrightarrow P$，$Pf_5Q\Leftrightarrow Q\nrightarrow P$，$Pf_6Q\Leftrightarrow Q$，$Pf_7Q\Leftrightarrow P\oplus Q$，$Pf_8Q\Leftrightarrow P\lor Q$，$Pf_9Q\Leftrightarrow P\downarrow Q$，$Pf_{10}Q\Leftrightarrow P\leftrightarrow Q$，$Pf_{11}Q\Leftrightarrow\lnot Q$，$Pf_{12}Q\Leftrightarrow Q\rightarrow P$，$Pf_{13}Q\Leftrightarrow\lnot P$，$Pf_{14}Q\Leftrightarrow P\rightarrow Q$，$Pf_{15}Q\Leftrightarrow P\uparrow Q$，$Pf_{16}Q\Leftrightarrow T$
   可见，对于二元运算符的每一种运算结果都可以用以上 9 中联结词表达

但是这 9 个联结词并非相互独立的，某些联结词可以用另外一些联结词等价表示，如 $P\rightarrow Q\Leftrightarrow\lnot P\lor Q$

由等价公式

$$\begin{aligned} P\rightarrow Q&\Leftrightarrow\lnot P\lor Q\\ P\leftrightarrow Q&\Leftrightarrow(P\rightarrow Q)\land(Q\rightarrow P)\\ P\nrightarrow Q&\Leftrightarrow\lnot(P\rightarrow Q)\\ P\oplus Q&\Leftrightarrow\lnot(P\leftrightarrow Q)\\ P\downarrow Q&\Leftrightarrow\lnot(P\lor Q)\\ P\uparrow Q&\Leftrightarrow\lnot(P\land Q) \end{aligned}$$

知：

• $\downarrow$ 可用 $\{\lnot,\ \lor\}$ 表示
• $\uparrow$ 可用 $\{\lnot,\ \land\}$ 表示
• $\oplus$ 可用 $\{\lnot,\ \leftrightarrow\}$ 表示
• $\leftrightarrow$ 可用 $\{\rightarrow,\ \land\}$ 表示
• $\rightarrow$ 可用 $\{\lnot,\ \lor\}$ 表示

又由徳·摩根定律可知：

• $\land$ 可用 $\{\lnot,\ \lor\}$ 表示
• $\lor$ 可用 $\{\lnot,\ \land\}$ 表示

因此任意命题公式都可由联结词集合 $\{\lnot,\ \lor\}$ 或 $\{\lnot,\ \land\}$ 等价表示

全功能联结词集合

对于一个联结词集合，如果所有命题公式都能由其中的联结词等价表示，则称此联结词集合为全功能联结词集合，又称此联结词集合是功能完备的

极小全功能联结词集合

对于一个极小全功能联结词集合，需满足两个条件：

1. 该联结词集合是全功能联结词集合
2. 去掉其中任意一个联结词所得的联结词集合都不是全功能联结词集合

常见的极小全功能联结词集合有，$\{\lnot,\ \lor\}$、$\{\lnot,\ \land\}$、$\{\downarrow\}$、$\{\uparrow\}$

命题公式

定义

命题公式，又称命题合式公式，下面是其归纳定义：

1. 基础条款：单个命题常元或命题变元是命题公式
2. 归纳条款
   • 若 $A$ 是命题公式，则 $\lnot A$ 是命题公式
   • 若 $A$ 和 $B$ 是命题公式，则 $A\land B$、$A\lor B$、$A\rightarrow B$、$A\leftrightarrow B$ 是命题公式
3. 极小性条款：只有有限次地应用条款 1 和条款 2 生成的表达式才是命题公式

命题公式常用大写字母 $A,B,C,\cdots$ 表示
需要注意的是不要把命题和命题公式弄混了
如：命题 $A,\ B,\ C$ 组成的命题公式 $(A\lor B)\rightarrow C$ 可用 $P$ 代表此公式

命题公式不是命题，没有真值，只有对其进行赋值后才有真值

命题的符号化

将自然语言命题写成与之内涵相同的命题公式称为命题的符号化

下面演示如何将命题符号化：
设 $P$：明天下雨，$Q$：明天下雪，$R$：我去上课
可以用命题公式 $(P\lor Q)\rightarrow \lnot R$ 表示命题 “如果明天下雨或下雪，那么我不去上课”

子公式

若 $B$ 是命题公式 $A$ 的一个连续段且 $B$ 是命题公式，则称 $B$ 是 $A$ 的子公式

如：命题公式 $(P\land Q)\rightarrow(\lnot P\lor(P\leftrightarrow Q))$ 的子公式有 $P$、$Q$、$P\land Q$、$\lnot P$、$P\leftrightarrow Q$、$\lnot P\lor (P\leftrightarrow Q)$
但 $(P\land Q)\rightarrow$ 并非子公式，因为它不是命题公式

赋值

命题公式的真值由其所含命题变元的真值决定

为命题公式中的所有命题变元指定一组真值称为对该命题公式赋值（指派、解释）

若一个命题公式含有 $n$ 个命题变元，那么它就有 $2^n$ 种不同的赋值，因为每个命题变元可以有 $F$ 和 $T$ 两个赋值

分类

依据命题公式的取值

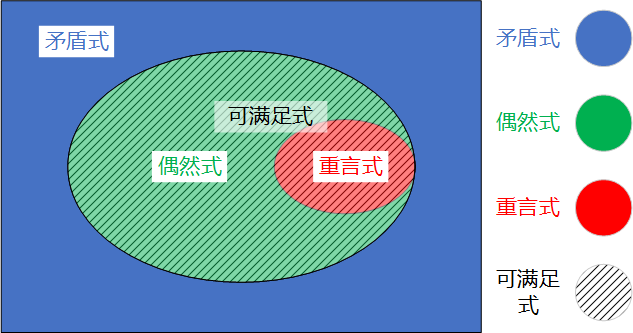
下面这幅文氏图表明了各种分类的关系：

可满足式=重言式+偶然式

重言式

若一个命题公式在任意赋值下，它的真值都为 $T$，则称该命题公式为重言式，又称永真式

矛盾式

若一个命题公式在任意赋值下，它的真值都为 $F$，则称该命题公式为矛盾式，又称永假式

偶然式

若一个命题公式有真值为 $T$ 的赋值，也有真值为 $F$ 的赋值，则称该命题公式为偶然式

可满足式

若一个命题公式至少有一个真值为 $T$ 的赋值，则称该命题公式为可满足式

等价与蕴含

等价

定义

$A,B$ 为两个命题公式，$P_1,P_2,\cdots,P_n$ 为所有出现在 $A,B$ 中的命题变元，但 $P_i,\ i=1,2,\cdots,n$ 不一定都同时出现在 $A$ 和 $B$ 中。若对于 $P_1,P_2,\cdots,P_n$ 的任意一组赋值，$A$ 和 $B$ 的真值都相同，则称 $A$ 和 $B$ 逻辑等价(logically equivalent)，记作 $A\Leftrightarrow B$，读作 “$A$ 等价于 $B$”

逻辑等价可类比为代数中的等于号

等价与双条件联结词的关系

$P$ 和 $Q$ 逻辑等价，当且仅当 $P\leftrightarrow Q$ 为重言式

证明过程

证明：
由双条件联结词的定义：$P\leftrightarrow Q$ 为真，当且仅当 $P$ 和 $Q$ 真值相同
而 $P\leftrightarrow Q$ 为重言式，即 $P\leftrightarrow Q$ 恒为真
可得 $P$ 和 $Q$ 真值相同
进而可得 $P$ 和 $Q$ 逻辑等价

常见等价公式

定律	公式
对合律	$\lnot\lnot P\Leftrightarrow P$
幂等律	$P\land P\Leftrightarrow P$ $P\lor P\Leftrightarrow P$
交换律	$P\land Q\Leftrightarrow Q\land P$ $P\lor Q\Leftrightarrow Q\lor P$
组合律	$P\land(Q\land R)\Leftrightarrow(P\land Q)\land R$ $P\lor(Q\lor R)\Leftrightarrow(P\lor Q)\lor R$
分配律	$P\land(Q\lor R)\Leftrightarrow(P\land Q)\lor(P\land R)$ $P\lor(Q\land R)\Leftrightarrow(P\lor Q)\land(P\lor R)$
德·摩根律	$\lnot(P\land Q)\Leftrightarrow\lnot P\lor\lnot Q$ $\lnot(P\lor Q)\Leftrightarrow\lnot P\land \lnot Q$
吸收律	$P\land(P\lor Q)\Leftrightarrow P$ $P\lor(P\land Q)\Leftrightarrow P$
蕴含律	$P\rightarrow Q\Leftrightarrow \lnot P\lor Q$
双条件律	$P\leftrightarrow Q\Leftrightarrow(P\rightarrow Q)\land(Q\rightarrow P)$
零一律	$P\land F\Leftrightarrow F$ $P\lor T\Leftrightarrow T$
同一律	$P\land T\Leftrightarrow P$ $P\lor F\Leftrightarrow P$
矛盾律	$P\land\lnot P\Leftrightarrow F$
排中律	$P\lor\lnot P\Leftrightarrow T$
输出律	$(P\land Q)\rightarrow R\Leftrightarrow P\rightarrow(Q\rightarrow R)$
归谬律	$(P\rightarrow Q)\land(P\rightarrow\lnot Q)\Leftrightarrow\lnot P$
逆反律	$P\rightarrow Q\Leftrightarrow\lnot Q\rightarrow\lnot P$

蕴含

定义

$P$ 和 $Q$ 是命题公式，若 $P\rightarrow Q$ 为重言式，则称 $P$ 蕴含 $Q$ ，记作 $P\Rightarrow Q$

蕴含与条件联结词的关系

见定义

蕴含和等价的关系

$P,Q$ 为命题公式，$P\Leftrightarrow Q$ 当且仅当 $P\Rightarrow Q$ 且 $Q\Rightarrow P$

因此常见等价公式同样适用于蕴含

性质

$A,B,C$ 为命题公式

• 若 $A\Rightarrow B$ 且 $A$ 为重言式，则 $B$ 也为重言式

  证明过程

  $\because A\Rightarrow B$
  $\therefore A\rightarrow B$ 为重言式
  $\because A$ 为重言式，即 $A$ 必为 $T$
  $\therefore B$ 也必为 $T$，即为重言式

• 若 $A\Rightarrow B$ 且 $A\Rightarrow C$，则 $A\Rightarrow(B\land C)$

  证明过程

  下面用肯定前件法证明
  $\because A\Rightarrow B,\ A\Rightarrow C$
  $\therefore A\rightarrow B,\ A\rightarrow C$ 为重言式
  $\therefore A$ 为 $T$ 时，$B,\ C$ 必为 $T$，$B\land C$ 为 $T$
  $\therefore A\Rightarrow(B\land C)$

• 若 $A\Rightarrow C$ 且 $B\Rightarrow C$，则 $(A\lor B)\Rightarrow C$

  证明过程

  下面用肯定前件法证明
  $\because A\Rightarrow C,\ B\Rightarrow C$
  $\therefore A\rightarrow C,\ B\rightarrow C$ 为重言式
  $\therefore A$ 为 $T$ 时，$C$ 必为 $T$；$B$ 为 $T$ 时，$C$ 必为 $T$
  $\therefore A\lor B$ 为 $T$ 时，$C$ 必为 $T$
  $\therefore (A\lor B)\Rightarrow C$

常见蕴含公式

定律	公式
直推式	$P\Rightarrow P$
化简式	$P\land Q\Rightarrow P$ $P\land Q\Rightarrow Q$
附加式	$P\Rightarrow P\lor Q$ $Q\Rightarrow P\lor Q$
变形附加式 1 （$P$ 用 $\lnot P$ 代入）	$\lnot P\Rightarrow P\rightarrow Q$ $Q\Rightarrow P\rightarrow Q$
变形附加式 2 （式 1 用逆反律）	$\lnot(P\rightarrow Q)\Rightarrow P$ $\lnot(P\rightarrow Q)\Rightarrow \lnot Q$
假言推理	$P\land(P\rightarrow Q)\Rightarrow Q$
拒取式	$\lnot Q\land(P\rightarrow Q)\Rightarrow \lnot P$
析取三段论	$\lnot P\land(P\lor Q)\Rightarrow Q$
前提三段论	$(P\rightarrow Q)\land (Q\rightarrow R)\Rightarrow (P\rightarrow R)$
构造性二难推理	$(P\lor Q)\land(P\rightarrow R)\land(Q\rightarrow S)\Rightarrow R\lor S$
破坏性二难推理	$(\lnot R\lor \lnot S)\land(P\rightarrow R)\land(Q\rightarrow S)\Rightarrow \lnot P\lor \lnot Q$
合取二难推理	$(P\land Q)\land(P\rightarrow R)\land(Q\rightarrow S)\Rightarrow R\land S$
逆条件附加	$(P\rightarrow Q)\Rightarrow(Q\rightarrow R)\rightarrow(P\rightarrow R)$
条件归并	$(P\rightarrow Q)\land(R\rightarrow S)\Rightarrow(P\land R)\rightarrow(Q\land S)$
双条件三段论	$(P\leftrightarrow Q)\land(Q\leftrightarrow R)\Rightarrow P\leftrightarrow R$
前后件附加	$P\rightarrow Q\Rightarrow(P\lor R)\rightarrow(Q\lor R)$ $P\rightarrow Q\Rightarrow(P\land R)\rightarrow(Q\land R)$

常用于证明 $A\Rightarrow B$ 的方法：

1. 肯定前件法
   假设 $A$ 为 $T$，若能推出 $B$ 也为 $T$，则 $A\Rightarrow B$

   因为 $A$ 为 $T$ 时，$B$ 必为 $T$，$A\rightarrow B$ 为 $T$
   而 $A$ 为 $F$ 时，$A\rightarrow B$ 为 $T$
   因此 $A\rightarrow B$ 为重言式
   

2. 否定后件法：
   假设 $B$ 为 $F$，若能推出 $A$ 也为 $F$，则 $A\Rightarrow B$

   $A\rightarrow B$ 为 $F$ 时，当且仅当 $A$ 为 $T$ 且 $B$ 为 $F$
   而我们得到 $B$ 为 $F$ 时，$A$ 必为 $F$。因此 $A\rightarrow B$ 为重言式

3. 真值表法
   列出 $A,B,A\rightarrow B$ 的真值表，证明 $A\rightarrow B$ 为重言式

三个规则

代入规则

$A,B,C$ 是命题公式，$P$ 为同时出现在 $A,B$ 中的命题变元。用 $C$ 代替 $P$（$A,B$ 中每次出现 $P$ 的地方都要用 $C$ 代替）得 $A^{'},B^{'}$

• 若 $A\Leftrightarrow B$，则 $A^{'}\Leftrightarrow B^{'}$
• 若 $A\Rightarrow B$，则 $A^{'}\Rightarrow B^{'}$

替换规则

$A,X,Y$ 是命题公式，$X$ 是 $A$ 的子公式，$X\Leftrightarrow Y$。若将 $A$ 中的 $X$ 用 $Y$ 替换（不必每一处都替换）后得 $B$，则 $A\Leftrightarrow B$

传递规则

$A,B,C$ 是命题公式

• 若 $A\Leftrightarrow B$ 且 $B\Leftrightarrow C$，则 $A\Leftrightarrow C$

  证明过程

  $\because A\Leftrightarrow B,\ B\Leftrightarrow C$
  $\therefore A$ 与 $B$、$B$ 与 $C$ 的真值相同
  $\therefore A$ 与 $C$ 的真值相同
  $\therefore A\Leftrightarrow C$

• 若 $A\Rightarrow B$ 且 $B\Rightarrow C$，则 $A\Rightarrow C$

  证明过程

  下面用肯定前件法证明
  $\because A\Rightarrow B,\ B\Rightarrow C$
  $\therefore A\rightarrow B,\ B\rightarrow C$ 为重言式
  $\therefore A$ 为 $T$ 时，$B$ 必为 $T$，$C$ 也必为 $T$
  $\therefore A\Rightarrow C$

对偶式

定义

设命题公式 $A$ 仅含有联结词 $\lnot,\ \land,\ \lor$。若将 $A$ 中 $\land$ 换成 $\lor$、$\lor$ 换成 $\land$，常元 $T$ 换成 $F$、$F$ 换成 $T$。替换后的命题公式记作 $A^*$，则称 $A^*$ 为 $A$ 的对偶公式，简称对偶式

性质

$A,\ B$ 为命题公式，联结词仅含有 $\lnot,\ \land,\ \lor$，$A^*,\ B^*$ 为其对偶式

• $\lnot A(P_1,P_2,\cdots,P_n)\Leftrightarrow A^*(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)$
  其中 $P_1,P_2,\cdots,P_n$ 是出现在 $A$ 中的所有命题变元

  证明过程

  由德·摩根定律知
  当减少 $\lnot$ 的辖域时，$\land$ 与 $\lor$ 互换、$T$ 和 $F$ 互换、$P_i$ 变为 $\lnot P_i$
  与对偶式的定义相比就是多了 $P_i$ 变为 $\lnot P_i$ 的过程

• 若 $A\Leftrightarrow B$，则 $A^*\Leftrightarrow B^*$

  证明过程

  设 $P_1,P_2,\cdots,P_n$ 为出现在 $A,\ B$ 的所有命题变元
  由代入规则知
  $A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow B(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)$
  $\because \lnot A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow A^*(P_1,P_2,\cdots,P_n)$
  $\therefore A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow\lnot A^*(P_1,P_2,\cdots,P_n)$
  同理得 $B(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow\lnot B^*(P_1,P_2,\cdots,P_n)$
  $\therefore \lnot A^*(P_1,P_2,\cdots,P_n)\Leftrightarrow\lnot B^*(P_1,P_2,\cdots,P_n)$，由传递规则
  $\therefore A^*(P_1,P_2,\cdots,P_n)\Leftrightarrow B^*(P_1,P_2,\cdots,P_n)$

• 若 $A\Rightarrow B$，则 $B^*\Rightarrow A^*$

  证明过程

  由代入规则知
  $A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Rightarrow B(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)$
  $\because \lnot A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow A^*(P_1,P_2,\cdots,P_n)$
  $\therefore A(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow\lnot A^*(P_1,P_2,\cdots,P_n)$
  同理得 $B(\lnot P_1,\lnot P_2,\cdots,\lnot P_n)\Leftrightarrow\lnot B^*(P_1,P_2,\cdots,P_n)$
  $\therefore \lnot A^*(P_1,P_2,\cdots,P_n)\Rightarrow \lnot B^*(P_1,P_2,\cdots,P_n)$
  由逆反律得
  $B^*\Rightarrow A^*$

范式

一个命题公式有多种等价表达形式，为了统一，需要将命题公式进行规范化

主析取范式

在了解主析取范式时需要先了解合取式和析取范式两个概念

合取式

若干个命题变元仅由联结词 $\{\lnot,\ \land\}$ 所组成的命题公式称为合取式

如：$P,\ P\land Q,\ \lnot P\land Q$ 都是合取式

注意：合取式不含命题常元

析取范式

析取范式具有如下形式：

$$A_1\lor A_2\lor\cdots\lor A_n~~~~(n\geq 1)$$

其中，$A_1,A_2,\cdots,A_n$ 为合取式

析取范式不唯一

如：$(P\land\lnot P)\lor(\lnot P\land Q)\lor(P\land\lnot Q)$ 是析取范式
但是它的另一种等价形式 $(\lnot P\land Q)\lor(P\land\lnot Q)$ 也是析取范式

极小项

若一个命题公式为合取式，且满足其中每个命题变元与其否定不能同时出现，但必出现其一，则称该合取式为极小项

若干个命题变元能组成极小项的个数：

1. 两个命题变元 $P,\ Q$ 组成的极小项有四个，分别为
   $\lnot P\land\lnot Q$、$\lnot P\land Q$、$P\land\lnot Q$、$P\land Q$
2. $n$ 个命题变元 $P_1,P_2,\cdots,P_n$ 组成的极小项有 $2^n$ 个，分别为
   $\widetilde P_1\land\widetilde P_2\land\cdots\land\widetilde P_n$
   其中 $\widetilde P_i$ 要么为 $P_i$ 要么为 $\lnot P_i$

极小项的编码：
可以将 $n$ 个命题变元组成的极小项编码成长度为 $n$ 的二进制串

• $\widetilde P_i$ 取 $\lnot P_i$ 时，二进制串第 $i$ 位取值为 $0$
• $\widetilde P_i$ 取 $P_i$ 时，二进制串第 $i$ 位取值为 $1$

以两个命题变元 $P,\ Q$ 为例：

• $m_0=m_{00}=\lnot P\land\lnot Q$
• $m_1=m_{01}=\lnot P\land Q$
• $m_2=m_{10}= P\land\lnot Q$
• $m_3=m_{11}= P\land Q$

$P$	$Q$	$\lnot P\land\lnot Q$	$\lnot P\land Q$	$P\land\lnot Q$	$P\land Q$
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

极小项有以下性质：

• 唯一性。没有两个极小项是等价的
• 只有与其二进制编码串一样的赋值才能使其值为 $T$，其余都为 $F$
• 任意两个不同的极小项的合取为矛盾式
• 所有极小项的析取为重言式

定义

主析取范式具有如下形式：

$$A_1^{'}\lor A_2^{'}\lor\cdots\lor A_n^{'}~~~~(n\geq 1)$$

其中，$A_1^{'},A_2^{'},\cdots,A_n^{'}$ 为极小项

对于命题公式 $A$，若由其所有命题变元所构成的主析取范式与 $A$ 等价，则称此主析取范式为命题公式 $A$ 的主析取范式

如：$P\leftrightarrow Q$ 的主析取范式为 $(\lnot P\land\lnot Q)\lor(P\land Q)$
$\begin{aligned} P\leftrightarrow Q&\Leftrightarrow(P\rightarrow Q)\land(Q\rightarrow P)\\ &\Leftrightarrow(\lnot P\lor Q)\land(\lnot Q\lor P)\\ &\Leftrightarrow[(\lnot P\lor Q)\land\lnot Q]\lor[(\lnot P\lor Q)\land P]\\ &\Leftrightarrow[(\lnot P\land\lnot Q)\lor(Q\land\lnot Q)]\lor[(\lnot P\land P)\lor(Q\land P)]\\ &\Leftrightarrow(\lnot P\land\lnot Q)\lor(P\land Q) \end{aligned}$
命题公式 $A$ 的主析取范式可以表示为

• $m_{00}\lor m_{11}$
• $m_{0}\lor m_{3}$
• $\sum(0,\ 3)$

求法

设有命题公式 $A$，需求出它的主析取范式

• 等价变换法
  用等价变换直接推导出 $A$ 的主析取范式

• 真值表法
  在 $A$ 的真值表中，使 $A$ 真值为 $T$ 的所有赋值所对应的极小项构成的析取范式为 $A$ 的主析取范式

  原因理解

  因为极小项只有一个赋值使其真值为 $T$
  而极小项之间的析取其实就是增加真值为 $T$ 的赋值
  $A$ 所有真值为 $T$ 所对应的极小项的析取的真值表自然与 $A$ 一样

主合取范式

在了解主合取范式时需要先了解析取式和合取范式两个概念

析取式

若干个命题变元仅由联结词 $\{\lnot,\ \lor\}$ 所组成的命题公式称为析取式

如：$P,\ P\lor Q,\ \lnot P\lor Q$ 都是析取式

注意：析取式不含命题常元

合取范式

合取范式具有如下形式：

$$A_1\land A_2\land\cdots\land A_n~~~~(n\geq 1)$$

其中，$A_1,A_2,\cdots,A_n$ 为析取式

合取范式也不唯一

如：$(P\lor\lnot P)\land(\lnot P\lor Q)\land(P\lor\lnot Q)$ 是合取范式
但是它的另一种等价形式 $(\lnot P\land Q)\lor(P\land\lnot Q)$ 也是合取范式

极大项

若一个命题公式为析取式，且满足其中每个命题变元与其否定不能同时出现，但必出现其一，则称该析取式为极大项

若干个命题变元能组成极大项的个数：

1. 两个命题变元 $P,\ Q$ 组成的极大项有四个，分别为
   $\lnot P\lor\lnot Q$、$\lnot P\lor Q$、$P\lor\lnot Q$、$P\lor Q$
2. $n$ 个命题变元 $P_1,P_2,\cdots,P_n$ 组成的极小项有 $2^n$ 个，分别为
   $\widetilde P_1\lor\widetilde P_2\lor\cdots\lor\widetilde P_n$
   其中 $\widetilde P_i$ 要么为 $P_i$ 要么为 $\lnot P_i$

极大项的编码：
与极小项一样，也可以将 $n$ 个命题变元组成的极大项编码成长度为 $n$ 的二进制串，不过不同的是：

• $\widetilde P_i$ 取 $\lnot P_i$ 时，二进制串第 $i$ 位取值为 $1$
• $\widetilde P_i$ 取 $P_i$ 时，二进制串第 $i$ 位取值为 $0$

以两个命题变元 $P,\ Q$ 为例：

• $M_0=M_{00}=P\lor Q$
• $M_1=M_{01}=P\lor\lnot Q$
• $M_2=M_{10}=\lnot P\lor Q$
• $M_3=M_{11}=\lnot P\lor\lnot Q$

$P$	$Q$	$P\lor Q$	$P\lor\lnot Q$	$\lnot P\lor Q$	$\lnot P\lor\lnot Q$
0	0	0	1	1	1
0	1	1	0	1	1
1	0	1	1	0	1
1	1	1	1	1	0

极大项有以下性质：

• 唯一性。没有两个极大项是等价的
• 只有与其二进制编码串一样的赋值才能使其值为 $F$，其余都为 $T$
• 任意两个不同的极大项的析取为重言式
• 所有极大项的合取为矛盾式

定义

主合取范式具有如下形式：

$$A_1^{'}\land A_2^{'}\land\cdots\land A_n^{'}~~~~(n\geq 1)$$

其中，$A_1^{'},A_2^{'},\cdots,A_n^{'}$ 为极大项

对于命题公式 $A$，若由其所有命题变元所构成的主合取范式与 $A$ 等价，则称此主合取范式为命题公式 $A$ 的主合取范式

如：$P\leftrightarrow Q$ 的主合取范式为 $(P\lor\lnot Q)\land(\lnot P\lor Q)$
$\begin{aligned} P\leftrightarrow Q&\Leftrightarrow(P\rightarrow Q)\land(Q\rightarrow P)\\ &\Leftrightarrow(\lnot P\lor Q)\land(\lnot Q\lor P)\\ &\Leftrightarrow(P\lor\lnot Q)\land(\lnot P\lor Q) \end{aligned}$
命题公式 $A$ 的主合取范式可以表示为

• $M_{01}\land M_{10}$
• $M_{1}\land M_{2}$
• $\prod(1,\ 2)$

求法

设有命题公式 $A$，需求出它的主合取范式

• 等价变换法
  用等价变换直接推导出 $A$ 的主合取范式

• 真值表法
  在 $A$ 的真值表中，使 $A$ 真值为 $F$ 的所有赋值所对应的极大项构成的合取范式为 $A$ 的主合取范式

  原因理解

  因为极大项只有一个赋值使其真值为 $F$
  而极大项之间的合取其实就是增加真值为 $F$ 的赋值
  $A$ 所有真值为 $T$ 所对应的极大项的合取的真值表自然与 $A$ 一样

极小项与极大项的关系

对于极小项 $m_i$ 以及极大项 $M_i$，有

$$\lnot m_i\Leftrightarrow M_i$$

主析取范式和主合取范式的关系

由 $n$ 个命题变元构成的命题公式 $A$ 的主析取范式为 $\sum(i_1,i_2,\cdots,i_k)$、主合取范式为 $\prod(j_1,j_2,\cdots,j_t)$，则有

• $\{i_1,i_2,\cdots,i_k\}\cup\{j_1,j_2,\cdots,j_t\}=\{0,1,\cdots,2^n-1\}$
• $\{i_1,i_2,\cdots,i_k\}\cap\{j_1,j_2,\cdots,j_t\}=\varnothing$

证明过程

由题知

$$\begin{aligned} A&\Leftrightarrow m_{i_1}\lor m_{i_2}\lor\cdots\lor m_{i_k}\\ &\Leftrightarrow M_{j_1}\land M_{j_2}\land\cdots\land M_{j_t} \end{aligned}$$

$\therefore \lnot A\Leftrightarrow\lnot M_{j_1}\lor\lnot M_{j_2}\lor\cdots\lor\lnot M_{j_t}\Leftrightarrow m_{j_1}\lor m_{j_2}\lor\cdots\lor m_{j_t}$
$\because A\lor\lnot A\Leftrightarrow T$
$\therefore(m_{i_1}\lor m_{i_2}\lor\cdots\lor m_{i_k})\lor(m_{j_1}\lor m_{j_2}\lor\cdots\lor m_{j_t})\Leftrightarrow T$
$\because$ 所有极小项的析取才为重言式
$\therefore \{i_1,i_2,\cdots,i_k\}\cup\{j_1,j_2,\cdots,j_t\}=\{0,1,\cdots,2^n-1\}$
$\because A\land\lnot A\Leftrightarrow F$
$\begin{aligned}\therefore\ &(m_{i_1}\lor m_{i_2}\lor\cdots\lor m_{i_k})\land(m_{j_1}\lor m_{j_2}\lor\cdots\lor m_{j_t})\\&\Leftrightarrow(m_{i_1}\land m_{j_1})\lor(m_{i_1}\land m_{j_2})\lor\cdots\lor(m_{i_1}\land m_{j_t})\\&~~~~\lor(m_{i_2}\land m_{j_1})\lor(m_{i_2}\land m_{j_2})\lor\cdots\lor(m_{i_2}\land m_{j_t})\\&~~~~\lor\cdots\lor(m_{i_k}\land m_{j_1})\lor(m_{i_k}\land m_{j_2})\lor\cdots\lor(m_{i_k}\land m_{j_t})\\&\Leftrightarrow F\end{aligned}$
$\therefore m_{i_a}\land m_{j_b}\Leftrightarrow F$ 其中 $a\in\{1,2\cdots k\}$，$b\in\{1,2,\cdots,t\}$
$\because$ 不同极小项的合取为矛盾式
$\therefore i_a\neq j_b$
$\therefore \{i_1,i_2,\cdots,i_k\}\cap\{j_1,j_2,\cdots,j_t\}=\varnothing$

因此只要求出命题公式 $A$ 的主析取范式和主合取范式二者之一，就可由此求出另一个
如：已知 $P\leftrightarrow Q$ 的主合取范式为 $\prod(1,2)$，则可知其主析取范式为 $\sum(0,3)$

命题逻辑的推理理论

推理

$H_1,H_2,\cdots,H_n,\ C$ 是命题公式，若满足 $H_1\land H_2\land\cdots\land H_n\Rightarrow C$ 则，

• 称 $C$ 为前提 $H_1,H_2,\cdots,H_n$ 的有效结论
  或称 $C$ 可由前提 $H_1,H_2,\cdots,H_n$ 逻辑推出
• 称从前提 $H_1,H_2,\cdots,H_n$ 推出结论 $C$ 的过程为推理、论证或证明

为简化书写，也将 $H_1\land H_2\land\cdots\land H_n\Rightarrow C$ 写作 $H_1,H_2,\cdots,H_n\Rightarrow C$

推理规则

公认规则

常见等价公式和蕴含公式

P 规则

推导过程中，前提可以在任何步骤引入

T 规则

推导过程中，由已知公式推出的结论可引入推导过程

推理方法

无义证明法

证明前提 $P$ 为矛盾式，则有 $P\rightarrow Q$ 为重言式，即 $P\Rightarrow Q$

平凡证明法

证明结论 $Q$ 为重言式，则有 $P\rightarrow Q$ 为重言式，即 $P\Rightarrow Q$

直接证明法

从前提出发，利用推理规则逻辑演绎得到有效结论

归谬法（反证法）

证明 $H_1\land H_2\land\cdots\land H_n\land\lnot C$ 为矛盾式

CP 规则法

对于 $(H_1\land H_2\land\cdots\land H_n)\Rightarrow(R\rightarrow C)$ 形式的推理
可采用间接的方法，即将前件 $R$ 作为附加前提，证明
$H_1\land H_2\land\cdots\land H_n\land R\Rightarrow C$ 即得证

证明过程

$\because H\Rightarrow(R\rightarrow C)$
$\therefore H\rightarrow(R\rightarrow C)$ 为重言式
$\because$ 输出律：$P\rightarrow(Q\rightarrow R)\Leftrightarrow(P\land Q)\rightarrow R$
$\therefore(H\land R)\rightarrow C$ 也为重言式
$\therefore(H\land R)\Rightarrow C$

命题逻辑的缺陷

命题逻辑能对自然语言中的逻辑思维进行精确的形式化描述，且能对一些较复杂的逻辑推理用形式化的方法证明。但是由于命题逻辑以简单命题为演算的基本单位，对简单命题不再分解，无法分析命题内部结构以及命题间的内在联系，导致命题逻辑在表示和推理方面存在局限性

• 表示方面
  如三个简单命题：老张是老师、小李是老师、大周是老师。在符号化时，必须得用到三个不同的符号，如：$P$：老张是老师、$Q$：小李是老师、$R$：大周是老师
• 推理方面
  如：“前提：所有人都是会死的；张三是人。结论：张三是会死的”。显然此推理是正确的，但是由于两个前提和一个结论都是简单命题，因此在命题逻辑中无法证明

参考

[1] 离散数学西安电子科技大学出版社第二版
[2] 命题常元百度百科
[3] 命题公式百度百科