无穷小
定义
若函数 f(x) 满足 x→x0(x→∞)limf(x)=0,则称 f(x) 为 x→x0(或 x→∞)时的无穷小
由定义可知无穷小的本质是一个函数,此函数在自变量的某一变化过程中函数值无限趋近于 0。无穷小并非一个很小的数
无穷小与极限的关系
x→x0(x→∞)limf(x)=A 的充分必要条件是 f(x)=A+α,其中 α 为 x→x0(或 x→∞)时的无穷小
此定理由极限的加法法则易证
无穷小的比较
当 x→0 时,x 和 x2 都是无穷小,但是 x→0limx2x=∞。因为在 x→0 过程中,x2 趋于 0 的速度比 x 快
根据两个无穷小之比的极限的不同情况,反映了不同无穷小趋于 0 的快慢程度
假设 α,β 为自变量的同一变化过程中的无穷小,根据 limβα 的取值
- 0:高阶无穷小
- 若存在 k>0 使 limβkα=c=0,则为 k 阶无穷小
- 不为 0 的常数:同阶无穷小
- ∞:低阶无穷小
高阶无穷小
若 limβα=0 则称“α 是比 β 高阶的无穷小”,记作 α=o(β)
低阶无穷小
若 limβα=∞ 则称“α 是比 β 低阶的无穷小”
若 α 是比 β 的高阶无穷小,则 β 是比 α 的低阶无穷小
同阶无穷小
若 limβα=c=0 则称“α 与 β 是同阶的无穷小”
k 阶无穷小
若 limβkα=c=0, k>0 则称“α 是关于 β 的 k 阶的无穷小”
等价无穷小
定义
若 limβα=1 则称“α 与 β 是等价无穷小”,记作 α∼β
性质
- 自反性:α∼α
- 对称性:若 α∼β 则 β∼α
- 传递性:若 α∼β, β∼γ 则 α∼γ
常见等价无穷小
x→0 时
-
sinx∼x
证明过程
如图单位圆内有一角度 x∈(−2π,0)∪(0,2π)
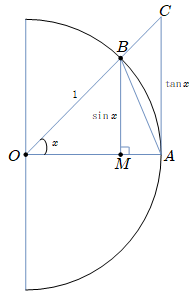
由图可看出当 x→0 时,始终有
S△AOB<S扇形AOB<S△AOC
∴21∣sinx∣<21∣x∣<21∣tanx∣
∴∣sinx∣<∣x∣<cosx∣sinx∣, cosx>0
∴cosx<∣xsinx∣<1
∴cosx<xsinx<1, xsinx>0
∵x→0limcosx=1
由夹逼准则知 x→0limxsinx=1
∴sinx∼x
-
tanx∼x
证明过程
∵
x→0limxtanx=x→0limxcosxsinx=x→0limxsinx⋅x→0limcosx1=1
∴tanx∼x
-
arcsinx∼x
证明过程
∵
x→0limxarcsinx=x→0lim(x)′(arcsinx)′=x→0lim1−x21=1
∴arcsinx∼x
-
ax−1∼xlna
证明过程
∵
x→0limxlnaax−1=x→0lim(xlna)′(ax−1)′=x→0limlnaaxlna=1
∴ax−1∼xlna
- ex−1∼x
- ln(1+x)∼x
-
1−cosx∼2x2
证明过程
> $\because$
> $$\begin{aligned}
> \lim\limits_{x\to 0}\frac{1-\cos x}{\frac{1}{2}x^2}&=\lim\limits_{x\to 0}\frac{(1-\cos x)'}{(\frac{1}{2}x^2)'}\\
> &=\lim\limits_{x\to 0}\frac{\sin x}{x}\\
> &=1
> \end{aligned}$$
> $\therefore 1-\cos x\sim\frac{1}{2}x^2$
-
(1+x)a−1∼ax
证明过程
∵
x→0limax(1+x)a−1=x→0lim(ax)′[(1+x)a−1]′=x→0limaa(1+x)a−1=1
∴(1+x)a−1∼ax
定理
定理 1:充要条件
α∼β 的充分必要条件为 β=α+o(α)
定理 2:等价替换
若 α∼β, α∼β 则 limβα=limβα=limβα=limβα
利用以上两个定理对于极限的求取很有帮助,如求极限 x→0limx+x2+x32x
因为 x=x+o(x),其中 o(x)=x2+x3
所以 x∼x+x2+x3
所以 x→0limx+x2+x32x=x→0limx2x=2
无穷大
若函数 f(x) 满足 x→x0(x→∞)limf(x)=∞,则称 f(x) 为 x→x0(或 x→∞)时的无穷大
注意:x→x0(x→∞)limf(x)=∞(①式)是 x→x0(x→∞)limf(x)=+∞(②式)和 x→x0(x→∞)limf(x)=−∞(③式)的统称。满足②③式其中之一必满足①式
由定义可知无穷大的本质是一个函数,此函数在自变量的某一变化过程中函数值无限趋近于 ∞。无穷大并非一个很大的数
无穷小与无穷大的关系
在自变量的同一变化过程中,
- 若 f(x) 为无穷小,则 f(x)1 为无穷大
- 若 f(x) 为无穷大,则 f(x)1 为无穷小
