几何定义
直角三角形定义
有一直角三角形如下
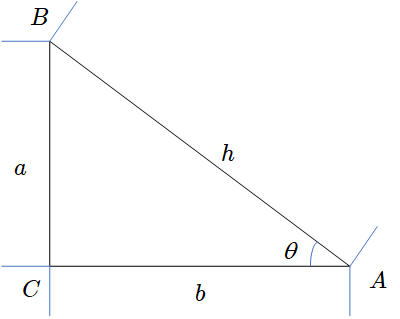
则三角函数定义如下
| 正弦 |
余弦 |
正切 |
余切 |
正割 |
余割 |
| sinθ=ha |
cosθ=hb |
tanθ=ba |
cotθ=ab |
secθ=bh |
cscθ=ah |
由于是直角三角形,因此此定义只能定义 θ∈(0,2π) 范围内
单位圆定义
有一单位圆 x2+y2=1 如下
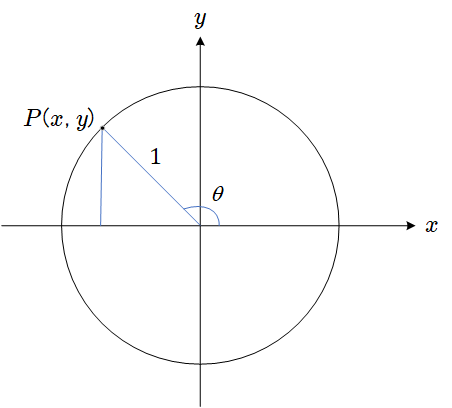
P(x,y) 为单位圆上一点
则三角函数定义如下
| 正弦 |
余弦 |
正切 |
余切 |
正割 |
余割 |
| sinθ=1y=y |
cosθ=1x=x |
tanθ=xy |
cotθ=yx |
secθ=x1 |
cscθ=y1 |
此时 θ∈(−∞,+∞)
- θ>0 时按逆时针旋转
- θ<0 时按顺时针旋转
函数图像
正弦函数
y=sinx
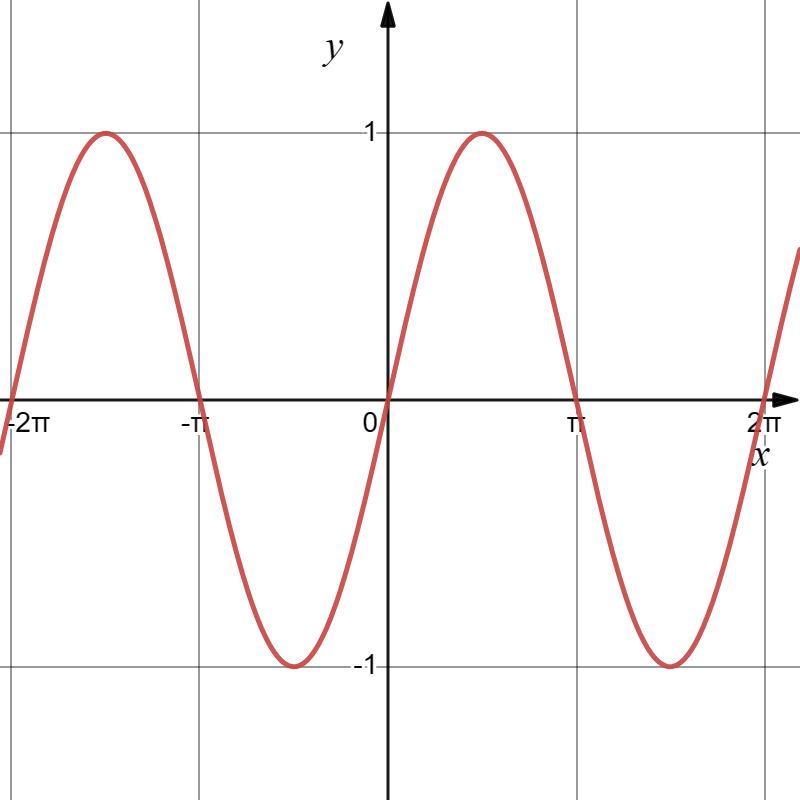
由图知正弦函数
- 最小正周期为 2π
- 对称轴为 x=2π+kπ, k∈Z
- 对称中心为 (kπ,0), k∈Z
- 在一二象限取值为正,三四象限取值为负
余弦函数
y=cosx
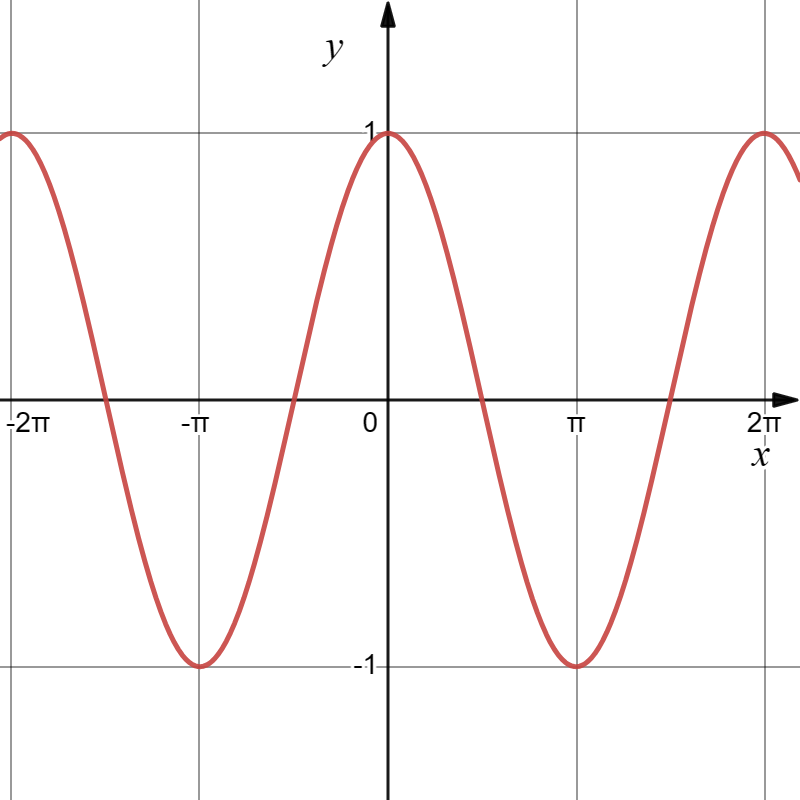
由图知余弦函数
- 最小正周期为 2π
- 对称轴为 x=kπ, k∈Z
- 对称中心为 (2π+kπ,0), k∈Z
- 在一四象限取值为正,二三象限取值为负
正切函数
y=tanx
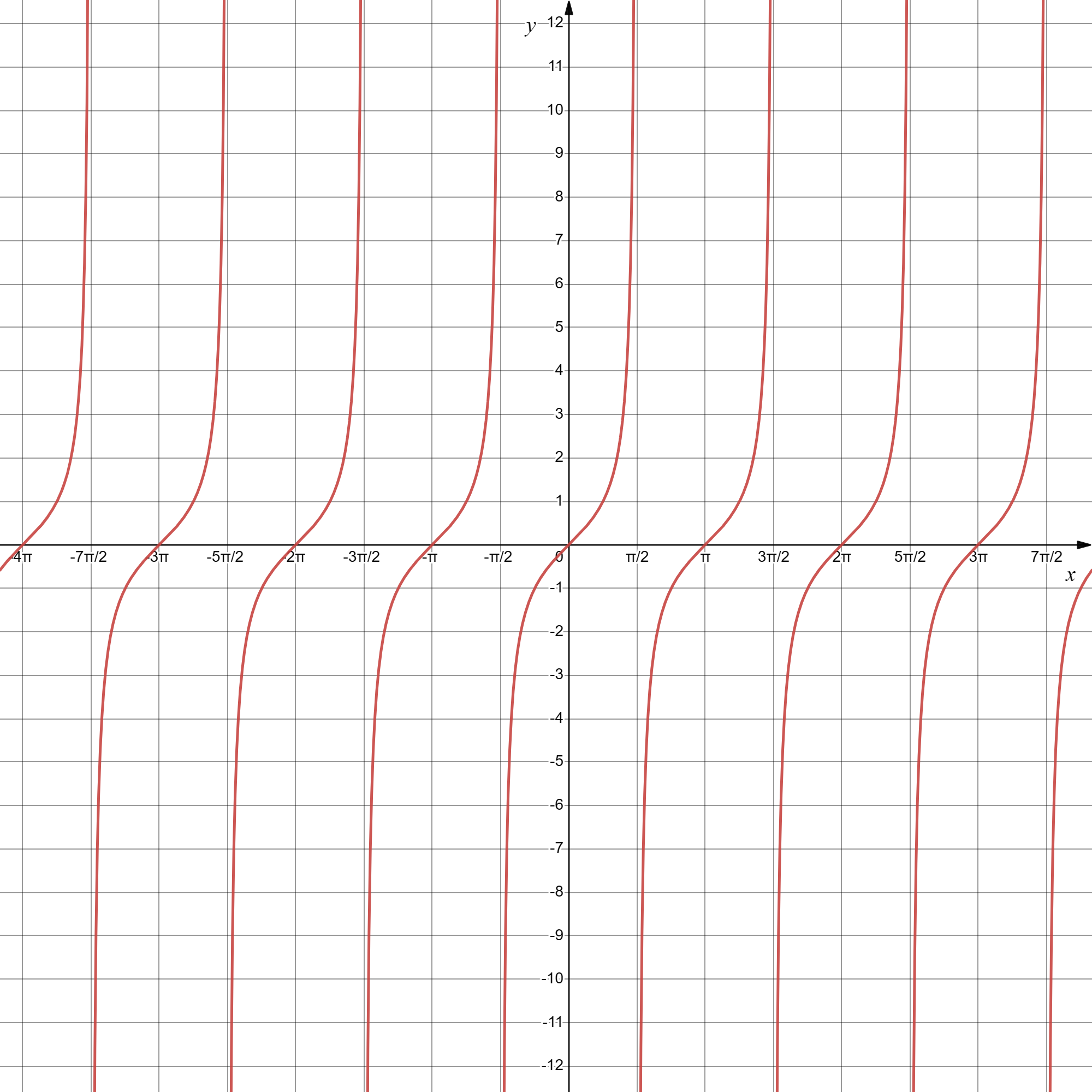
由图知正切函数
- 最小正周期为 π
- 对称中心为 (kπ,0), k∈Z
- 在一三象限取值为正、二四象限取值为负
余切函数
y=cotx
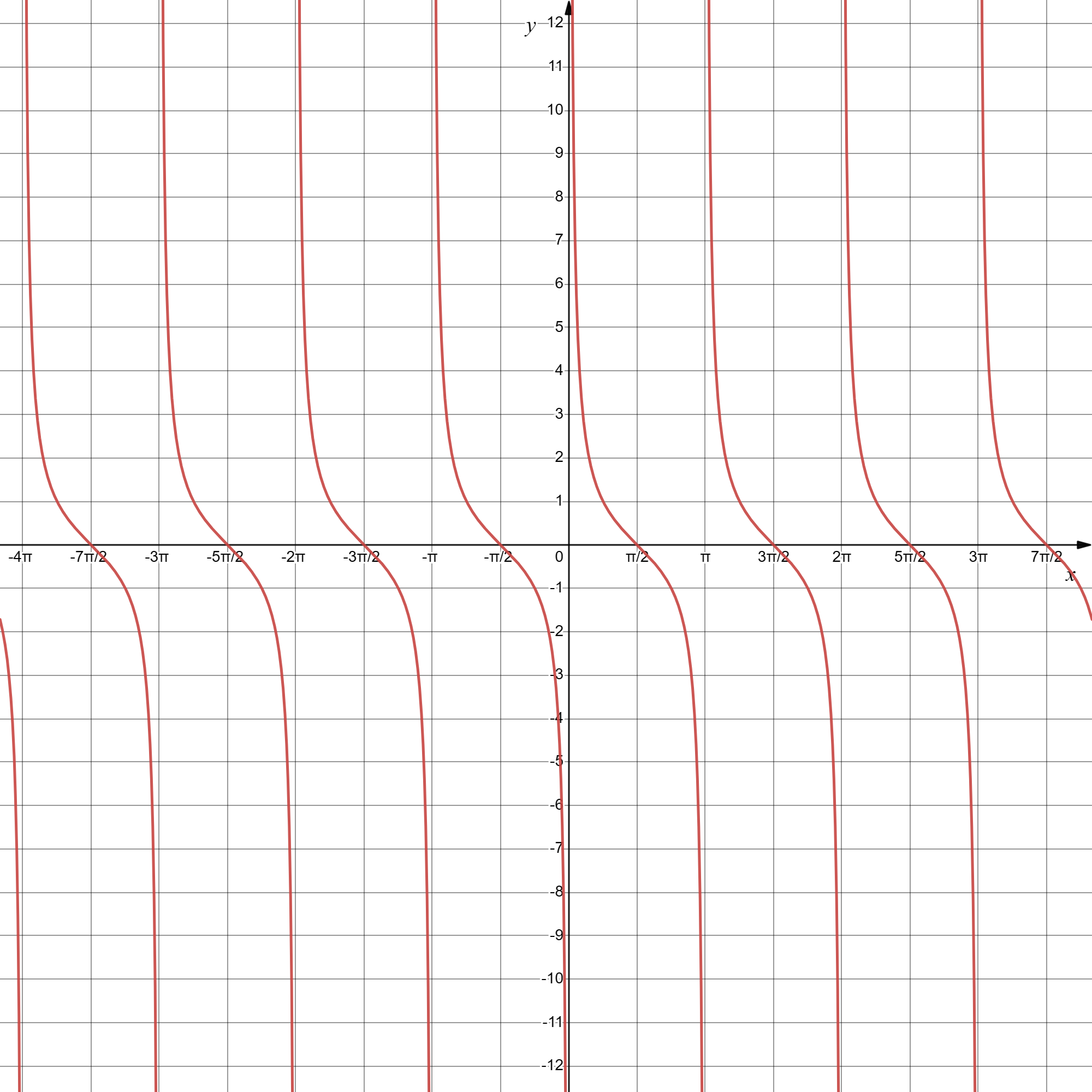
由图知余切函数
- 最小正周期为 π
- 对称中心为 (2π+kπ,0), k∈Z
- 在一三象限取值为正、二四象限取值为负
正割函数
y=secx
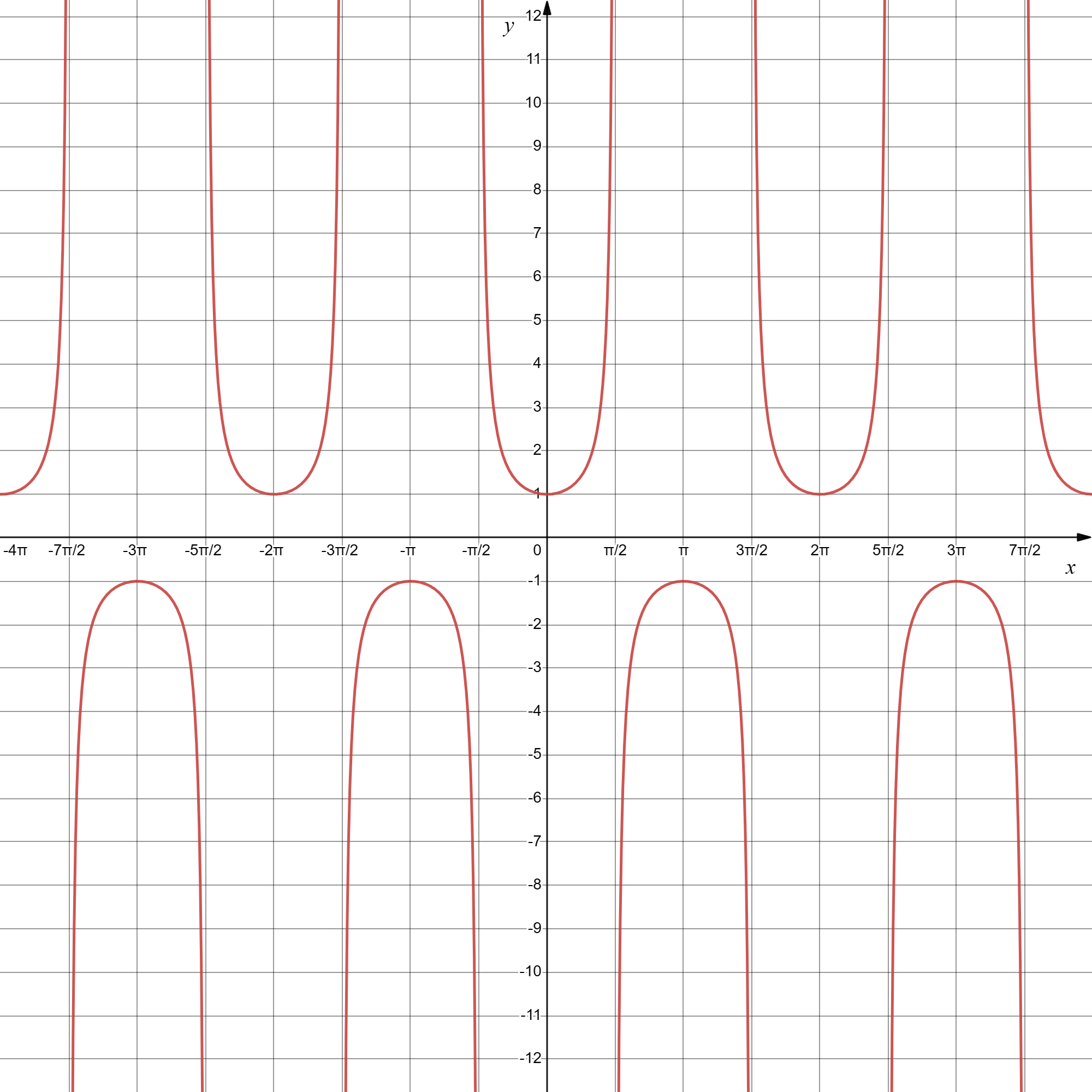
由图知正割函数
- 最小正周期为 2π
- 对称轴为 x=kπ, k∈Z
- 对称中心为 (2π+kπ,0), k∈Z
- 在一四象限取值为正、二三象限取值为负
余割函数
y=cscx
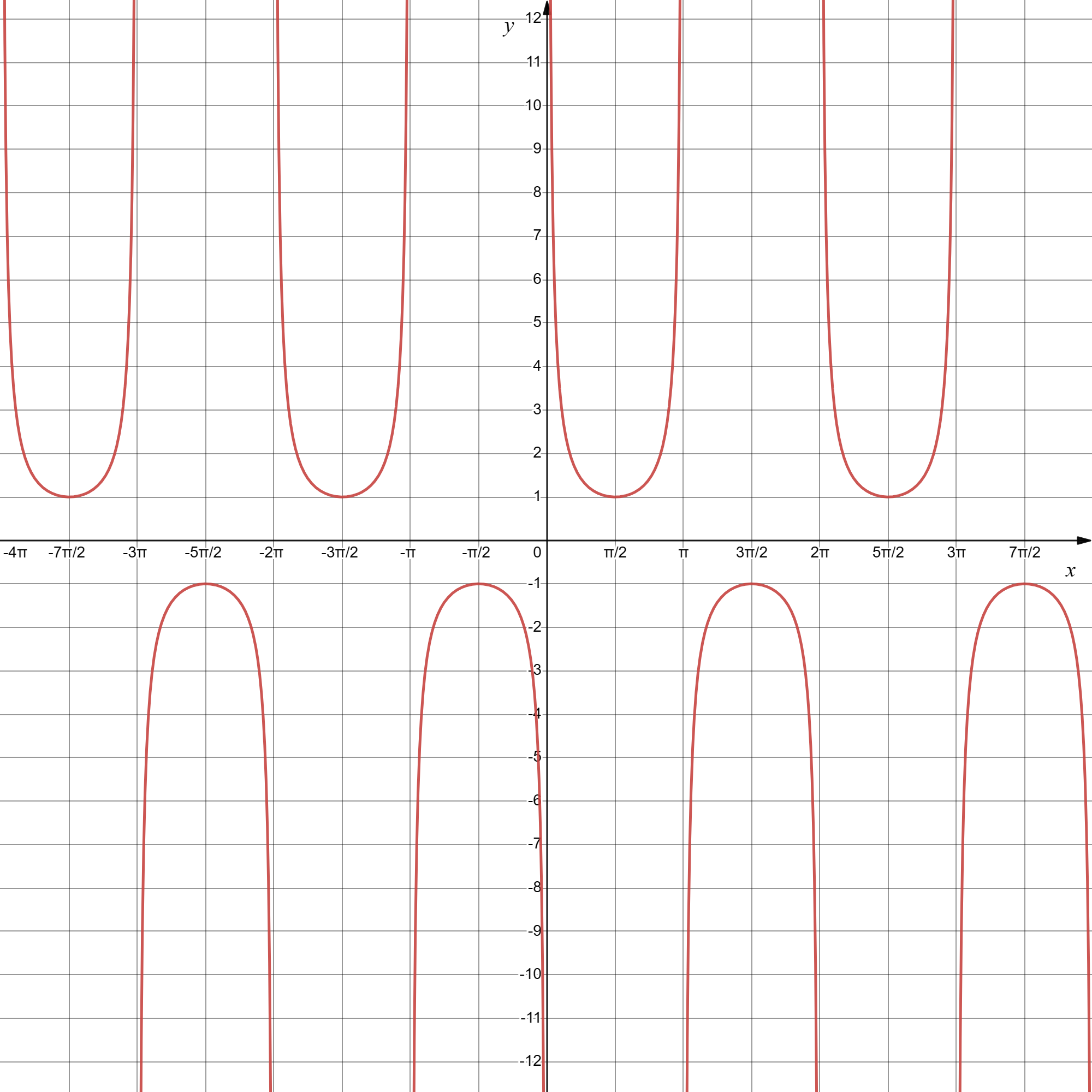
由图知余割函数
- 最小正周期为 2π
- 对称轴为 x=2π+kπ, k∈Z
- 对称中心为 (kπ,0), k∈Z
- 在一二象限取值为正、三四象限取值为负
恒等式
互相表示
由三角函数的定义可知
-
tanθ=cosθsinθ
-
cotθ=tanθ1=sinθcosθ
-
secθ=cosθ1
-
cscθ=sinθ1
毕达哥拉斯恒等式
由直角三角形定义和勾股定理或单位圆定义可知
- sin2θ+cos2θ=1
由此可推出
- tan2θ+1=sec2θ
- cot2θ+1=csc2θ
诱导公式
形如 sin/cos/tan/cot/sec/csc(θ+2kπ), k∈Z 其中“/”表示或者之意
变换口诀:奇变偶不变,符号看象限
- 奇偶的意思是 k 的奇偶性。若为奇数,则 sin 和 cos 互换、tan 和 cot 互换、sec 和 csc 互换;偶数则不变
- 将 θ 看作锐角,判断 θ+2kπ 所在象限。若在该象限下三角函数取负值,则在前面添加负号
如:
- sin(θ+2π)=cosθ
k=1 为奇数,sin 变 cos
θ+2π 在第二象限,sin 值为正,符号为正
- sin(θ+π)=−sinθ
k=2 为偶数,不需要变
θ+π 在第三象限,sin 值为负,符号为负
- cos(θ+23π)=sinθ
k=3 为奇数,cos 变 sin
θ+23π 在第四象限,cos 值为正,符号为正
- tan(θ−2π)=−cotθ
k=−1 为奇数,tan 变 cot
θ−2π 在第四象限,tan 值为负,符号为负
- sin(−θ)=−sinθ
k=0 为偶数,不需要变
−θ 在第四象限,sin 值为负,符号为负
以上结论由函数图形易得出
和差公式
正弦
- sin(θ1+θ2)=sinθ1cosθ2+cosθ1sinθ2
- sin(θ1−θ2)=sinθ1cosθ2−cosθ1sinθ2
证明过程
设有一单位圆 θ12+θ22=1
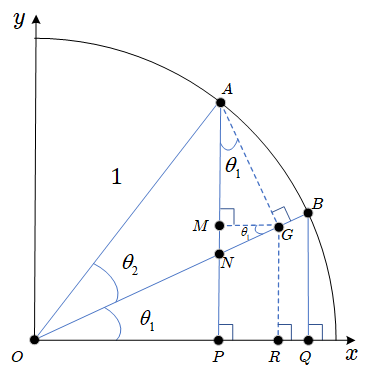
则 ∣AG∣=sinθ2, ∣OG∣=cosθ2
∴∣MP∣=∣GR∣=∣OG∣sinθ1=sinθ1cosθ2
∵△ONP∼△GNM(直角三角形一个角相等)
∴∠NGM=∠NOP=θ1
∵∠NGP+∠AGM=∠MAG+∠AGM=90°
∴∠MAG=∠NGM=θ1
∴∣AM∣=∣AG∣cosθ1=cosθ1sinθ2
∴
sin(θ1+θ2)=∣AP∣=∣AM∣+∣MP∣=sinθ1cosθ2+cosθ1sinθ2
令 θ2=−θ2 则
sin(θ1−θ2)=sin[θ1+(−θ2)]=sinθ1cos(−θ2)+cosθ1sin(−θ2)=sinθ1cosθ2−cosθ1sinθ2
余弦
- cos(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2
- cos(θ1−θ2)=cosθ1cosθ2+sinθ1sinθ2
证明过程
令 θ2=θ2+2π 则
cos(θ1+θ2)=sin(θ1+θ2+2π)=sinθ1cos(θ2+2π)+cosθ1sin(θ2+2π)=cosθ1cosθ2−sinθ1sinθ2
令 θ2=−θ2 则
cos(θ1−θ2)=cos[θ1+(−θ2)]=cosθ1cos(−θ2)−sinθ1sin(−θ2)=cosθ1cosθ2+sinθ1sinθ2
正切
tan(θ1+θ2)=1−tanθ1tanθ2tanθ1+tanθ2
tan(θ1−θ2)=1+tanθ1tanθ2tanθ1−tanθ2
证明过程
tan(θ1+θ2)=cos(θ1+θ2)sin(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2sinθ1cosθ2+cosθ1sinθ2=cosθ1cosθ2cosθ1cosθ2−cosθ1cosθ2sinθ1sinθ2cosθ1cosθ2sinθ1cosθ2+cosθ1cosθ2cosθ1sinθ2=1−cosθ1sinθ1cosθ2sinθ2cosθ1sinθ1+cosθ2sinθ2=1−tanθ1tanθ2tanθ1+tanθ2
令 θ2=−θ2 则
tan(θ1−θ2)=tan[θ1+(−θ2)]=1−tanθ1tan(−θ2)tanθ1+tan(−θ2)=1+tanθ1tanθ2tanθ1−tanθ2
倍角公式
由和差公式可推出
-
sin2θ=2sinθcosθ=sin2θ+cos2θ2sinθcosθ=1+tan2θ2tanθ
-
cos2θ=cos2θ−sin2θ=1+tan2θ1−tan2θ=2cos2θ−1=1−2sin2θ
-
tan2θ=1−tan2θ2tanθ
降幂公式
由倍角公式容易推出
由以上两个公式容易推出
半角公式
由倍角公式可推出
tan2θ=sinθ1−cosθ=1+cosθsinθ
证明过程
∵cosθ=1−2sin22θ
∴1−cosθ=2sin22θ
∵sinθ=2sin2θcos2θ
∴
sinθ1−cosθ=2sin2θcos2θ2sin22θ=cos2θsin2θ=tan2θ
∵cosθ=2cos22θ−1
∴1+cosθ=2cos22θ
∴
1+cosθsinθ=2cos22θ2sin2θcos2θ=cos2θsin2θ=tan2θ
积化和差公式
-
sinθ1sinθ2=−21[cos(θ1+θ2)−cos(θ1−θ2)]
-
sinθ1cosθ2=21[sin(θ1+θ2)+sin(θ1−θ2)]
-
cosθ1sinθ2=21[sin(θ1+θ2)−sin(θ1−θ2)]
-
cosθ1cosθ2=21[cos(θ1+θ2)+cos(θ1−θ2)]
证明过程
由和差公式得
⎩⎨⎧sin(θ1+θ2)=sinθ1cosθ2+cosθ1sinθ2sin(θ1−θ2)=sinθ1cosθ2−cosθ1sinθ2cos(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2cos(θ1−θ2)=cosθ1cosθ2+sinθ1sinθ2(1)(2)(3)(4)
式 (4)− 式 (3) 得
sinθ1sinθ2=21[cos(θ1−θ2)−cos(θ1+θ2)]
式 (4)+ 式 (3) 得
cosθ1cosθ2=21[cos(θ1+θ2)+cos(θ1−θ2)]
式 (1)+ 式 (2) 得
sinθ1cosθ2=21[sin(θ1+θ2)+sin(θ1−θ2)]
式 (1)− 式 (2) 得
cosθ1sinθ2=21[sin(θ1+θ2)−sin(θ1−θ2)]
和差化积公式
-
sinθ1+sinθ2=2sin(2θ1+θ2)cos(2θ1−θ2)
-
sinθ1−sinθ2=2cos(2θ1+θ2)sin(2θ1−θ2)
-
cosθ1+cosθ2=2cos(2θ1+θ2)cos(2θ1−θ2)
-
cosθ1−cosθ2=−2sin(2θ1+θ2)sin(2θ1−θ2)
证明过程
∵
θ1=2θ1+θ2+2θ1−θ2, θ2=2θ1+θ2−2θ1−θ2
∴
sinθ1=sin(2θ1+θ2)cos(2θ1−θ2)+cos(2θ1+θ2)sin(2θ1−θ2)sinθ2=sin(2θ1+θ2)cos(2θ1−θ2)−cos(2θ1+θ2)sin(2θ1−θ2)cosθ1=cos(2θ1+θ2)cos(2θ1−θ2)−sin(2θ1+θ2)sin(2θ1−θ2)cosθ2=cos(2θ1+θ2)cos(2θ1−θ2)+sin(2θ1+θ2)sin(2θ1−θ2)
∴
sinθ1+sinθ2=2sin(2θ1+θ2)cos(2θ1−θ2)
其他同理可证
辅助角公式
asinθ+bcosθ=a2+b2sin(θ+φ)
其中
sin(φ)=a2+b2b, cos(φ)=a2+b2a
参考
[1] 维基百科三角函数https://zh.wikipedia.org/wiki/三角函数
[2] 百度百科三角函数公式https://baike.baidu.com/item/三角函数公式/4374733








