反三角函数

定义

名称	符号	定义	定义域	值域
反正弦	$y=\arcsin x$	$x=\sin y$	$[-1,1]$	$[-\frac{\pi}{2},\frac{\pi}{2}]$
反余弦	$y=\arccos x$	$x=\cos y$	$[-1,1]$	$[0,\pi]$
反正切	$y=\arctan x$	$x=\tan y$	$\mathbb{R}$	$(-\frac{\pi}{2},\frac{\pi}{2})$

反正弦

函数 $f(x)=\sin x$ 在 $x\in[-\frac{\pi}{2},\frac{\pi}{2}]$ 部分的反函数 $f^{-1}(x)$ 称为反正弦函数，记作 $\arcsin x$

反余弦

函数 $f(x)=\cos x$ 在 $x\in[0,\pi]$ 部分的反函数 $f^{-1}(x)$ 称为反余弦函数，记作 $\arccos x$

反正切

函数 $f(x)=\tan x$ 在 $x\in(-\frac{\pi}{2},\frac{\pi}{2})$ 部分的反函数 $f^{-1}(x)$ 称为反正切函数，记作 $\arctan x$

图像

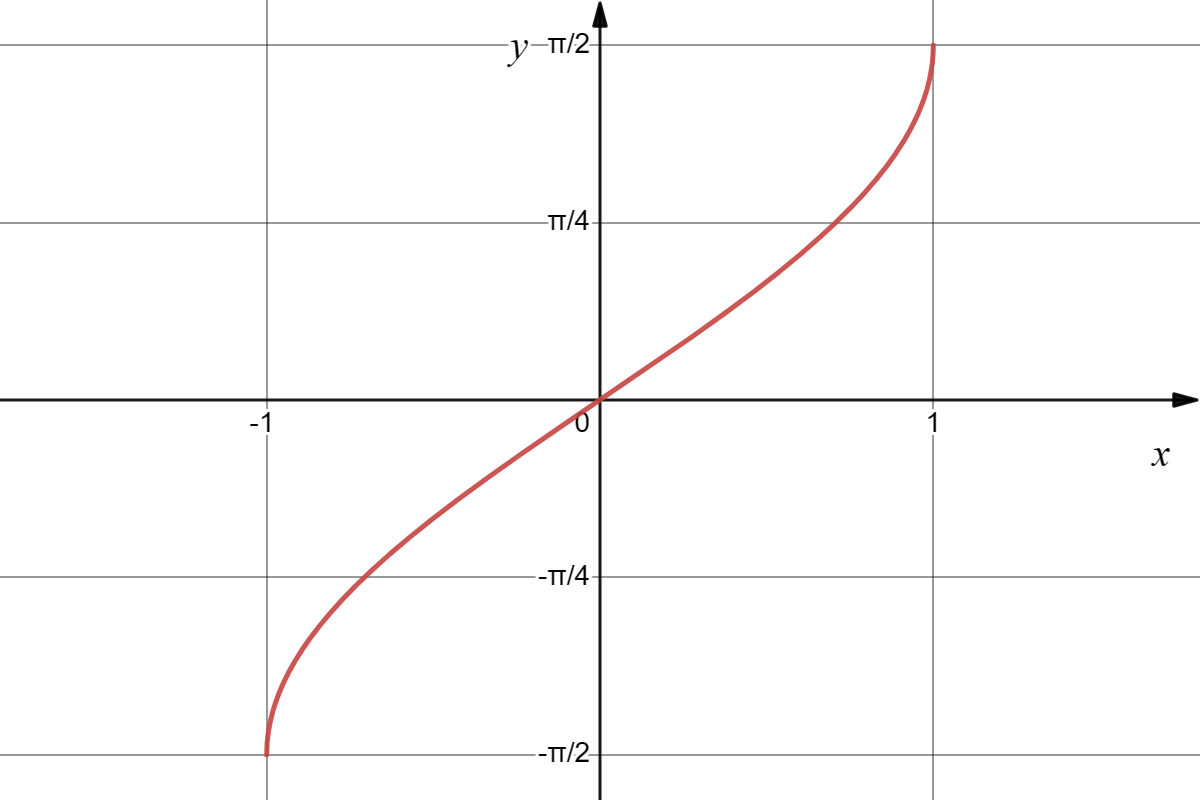
反正弦

$$y=\arcsin x$$

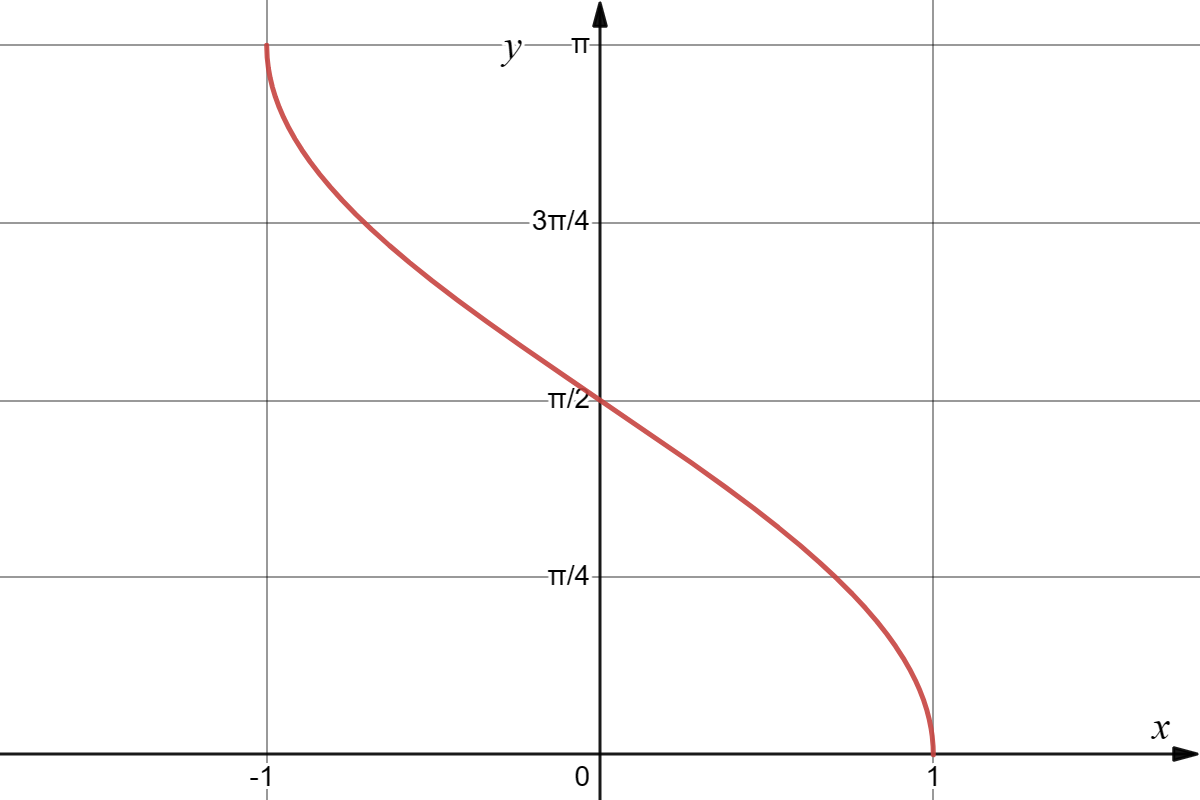
反余弦

$$y=\arccos x$$

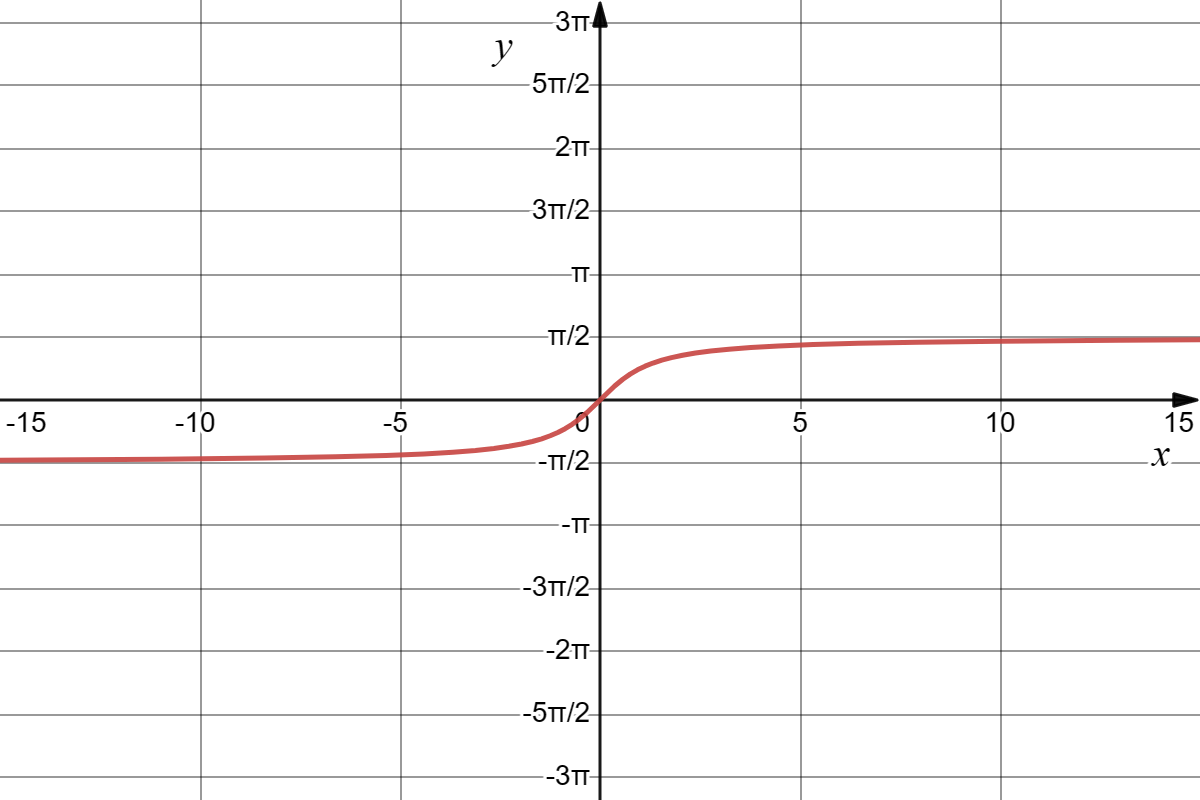
反正切

$$y=\arctan x$$

恒等式

余角

由 $y=\arcsin x$ 和 $y=\arccos x$ 的图像容易看出

$$\arcsin x+\arccos x=\frac{\pi}{2}$$

负数参数

• $\arcsin(-x)=-\arcsin x$
• $\arccos(-x)=\pi-\arccos x$
• $\arctan(-x)=-\arctan x$

参考

[1] 维基百科反三角函数https://zh.wikipedia.org/wiki/反三角函数